开放寻址的ThreadLocalMap分析

什么是散列

散列表(hash table)我们平时也叫它哈希表或者Hash表，它用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，没有数组就没有散列表。

比如我们有100件商品,编号没有规律的4位数字,现在我们想要通过编号快速获取商品信息，如何做呢?我们可以将这100件商品信息放到数组里，通过 商品编号%100这样的方式得到一个值,值为1的商品放到数组中下标为1的位置，值为2的商品，我们放到数组中下标为2的位置。以此类推，编号为K的选手放到数组中下标为K的位置。因为商品编号通过散列函数(编号%100)跟数据下标一一对应，所以但我们需要查询编号为x的商品信息的时候,我们使用同样的方式，将编号转换为数组下标，就可以从对应的数组下标的位置取出数据。
这就是散列的典型思想。

我们通过上面的例子可以得出这样规律：散列表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。通过散列函数(商品编号%100)把元素的键值映
射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取
数据。

开放寻址

一说到散列(或者叫做hash表),大家更熟悉的是HashMap或者LinkedHashMap,而今天的主角是ThreadLocalMap,它是ThreadLocal中的一个内部类。分析ThreadLocal源码的时候不可能绕过它。

由于哈希表使用了数组,无论hash函数如何设计都无可避免存在hash冲突。上面的例子如果两件商品的id分别是1001和1101,那么他们的数据就会就会被放到数组的同一个位置，出现了冲突

鸽巢原理，又名狄利克雷抽屉原理、鸽笼原理。其中一种简单的表述法为：若有n个笼子和n+1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少2只鸽子

ThreadLocalMap作为hash表的一种实现方式,它是使用什么方式来解决冲突的呢?它使用了开放寻址法来解决这个问题。

元素插入

开放寻址法的核心是如果出现了散列冲突，就重新探测一个空闲位置，将其插入。当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。

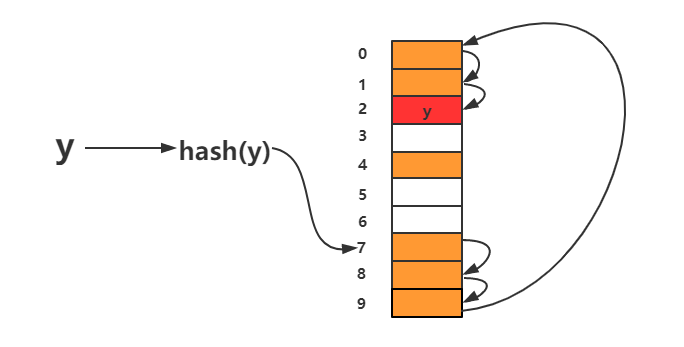
从图中可以看出，散列表的大小为 10 ，在元素 x 插入散列表之前，已经 6 个元素插入到散列表中。 x 经过 Hash 算法之后，被散列到位置下标为 7 的位置,但是这个位置已经有数据了，所以就产生了冲突。于是我们就顺序地往后一个一个找，看有没有空闲的位置，遍历到尾部都没有找到空闲的位置，于是我们再从表头开始找，直到找到空闲位置 2 ，于是将其插入到这个位置。

元素查找

在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中。

元素删除

ThreadLocalMap跟数组一样，不仅支持插入、查找操作，还支持删除操作。对于使用线性探测法解决冲突的散列表，删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。

还记得我们刚讲的查找操作吗？在查找的时候，一旦我们通过线性探测方法，找到一个空闲位置，我们就可以认定散列表中不存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。这个问题如何解决呢？

我们可以在删除元素之后,将之后不为null的数据rehash，这样就不会影响查询的逻辑

另一种方法是:可以将删除的元素，特殊标记为 deleted 。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测

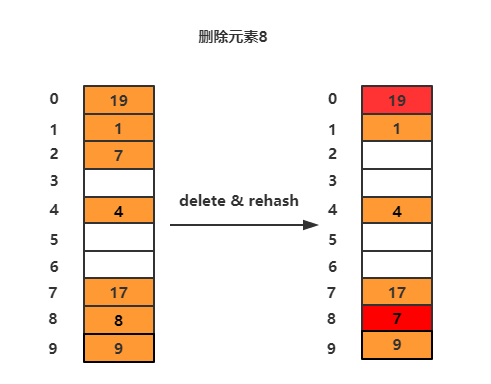
这里解释下rehash的过程:当删除元素8的时候，先把下标为8的值设置为null,然后将其后面不为空的数组元素rehash。比如8后面的元素是9,其原本应该的位置(9%10=9)就在9所以不移动。下一个元素是19,应该在下标为9的位置,但是已经被占用了,所以就找下一个空闲的位置，下标为3的位置是空闲的，放入tab[3]。接着下一个元素1就在tab[1]不移动，
元素7的位置在tab[7]，因为已经被占用，放入下一个空闲位置tab[8]。下一个元素仍然是19,这里由于tab[9]已经被占用，所以放入下一个空闲位置tab[0]。接着最后一个元素4位置就在tab[4],所以不移动。元素4的下一个位置为空，整个rehash过程结束。

装载因子

你可能已经发现了，线性探测法其实存在很大问题。当散列表中插入的数据越来越多时，散列冲突发生的可能性就会越来越大，空闲位置会越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，所以最坏情况下的时间复杂度为 O(n) 。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据。

不管采用哪种探测方法，hash函数设计得在合理,当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子(load factor)来表示空位的多少。

装载因子的计算公式是：散列表的装载因子=填入表中的元素个数/散列表的长度 装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。

源码分析

ThreadLocalMap定义

ThreadLocal的核心数据结构是ThreadLocalMap,它的数据结构如下：

static class ThreadLocalMap {
  
  // 这里的entry继承WeakReference了
  static class Entry extends WeakReference<ThreadLocal<?>> {
      Object value;
      Entry(ThreadLocal<?> k, Object v) {
          super(k);
          value = v;
      }
  }

  // 初始化容量,必须是2的n次方
  private static final int INITIAL_CAPACITY = 16;

  // entry数组,用于存储数据
  private Entry[] table;

  // map的容量
  private int size = 0;

  // 数据量达到多少进行扩容,默认是 table.length * 2 / 3
  private int threshold;

从ThreadLocalMap的定义可以看出Entry的key就是ThreadLocal，而value就是值。同时，Entry也继承WeakReference，所以说Entry所对应key（ThreadLocal实例）的引用为一个弱引用。而且定义了装载因子为数组长度的三分之二。

set()方法

private void set(ThreadLocal<?> key, Object value) {

  Entry[] tab = table;
  int len = tab.length;
  int i = key.threadLocalHashCode & (len-1);

  // 采用线性探测,寻找合适的插入位置
  for (Entry e = tab[i]; e != null; e = tab[i = nextIndex(i, len)]) {
      ThreadLocal<?> k = e.get();
      // key存在则直接覆盖
      if (k == key) {
          e.value = value;
          return;
      }
      // key不存在,说明之前的ThreadLocal对象被回收了
      if (k == null) {
          replaceStaleEntry(key, value, i);
          return;
      }
  }

  // 不存在也没有旧元素,就创建一个
  tab[i] = new Entry(key, value);
  int sz = ++size;
  // 清除旧的槽(entry不为空，但是ThreadLocal为空)，并且当数组中元素大于阈值就rehash
  if (!cleanSomeSlots(i, sz) && sz >= threshold)
    expungeStaleEntries();
    // 扩容
    if (size >= threshold - threshold / 4)
      resize();
}

上面源码的主要步骤如下:

1. 采用线性探测法,寻找合适的插入位置。首先判断key是否存在,存在则直接覆盖。如果key不存在证明被垃圾回收了此时需要用新的元素替换旧的元素
2. 不存在对应的元素,需要创建一个新的元素
3. 清除entry不为空，但是ThreadLocal(entry的key被回收了)的元素，防止内存泄露
4. 如果满足条件:size >= threshold - threshold / 4就将数组扩大为之前的两倍，同时会重新计算数组元素所处的位置并进行移动(rehash)。比如最开始数组初始大小为16,当size >= (16*2/3=10) - (10/4) = 8的时候就会扩容,将数组大小扩容至32.

无论是replaceStaleEntry()方法还是cleanSomeSlots()方法，最重要的方法调用是expungeStaleEntry(),你可以在ThreadLocalMap中的get,set,remove都能发现调用它的身影。

private int expungeStaleEntry(int staleSlot) {
  Entry[] tab = table;
  int len = tab.length;

  // 删除对应位置的entry
  tab[staleSlot].value = null;
  tab[staleSlot] = null;
  size--;

  Entry e;
  int i;

  // rehash过程,直到entry为null
  for (i = nextIndex(staleSlot, len);(e = tab[i]) != null; i = nextIndex(i, len)) {
    ThreadLocal<?> k = e.get();
    // k为空,证明已经被垃圾回收了
    if (k == null) {
        e.value = null;
        tab[i] = null;
        size--;
    } else {
        int h = k.threadLocalHashCode & (len - 1);
        // 判断当前元素是否处于"真正"应该待的位置
        if (h != i) {
            tab[i] = null;
            // 线性探测
            while (tab[h] != null)
                h = nextIndex(h, len);
            tab[h] = e;
        }
    }
  }
  return i;
}

上面rehash的代码结合文章开头的说明理解起来更是容易,当从ThreadLocalMap新增,获取,删除的时候都会根据条件进行rehash，条件如下

1. ThreadLocal对象被回收,此时Entry中key为null,value不为null。这时会触发rehash
2. 当阈值达到ThreadLocalMap容量的三分之二的时候

get()方法

private Entry getEntry(ThreadLocal<?> key) {
  int i = key.threadLocalHashCode & (table.length - 1);
  Entry e = table[i];
  // 现在数据中进行查找
  if (e != null && e.get() == key)
      return e;
  else
      return getEntryAfterMiss(key, i, e);
}

// 采用线性探测找到对应元素
private Entry getEntryAfterMiss(ThreadLocal<?> key, int i, Entry e) {
  Entry[] tab = table;
  int len = tab.length;

  while (e != null) {
      ThreadLocal<?> k = e.get();
      // 找到元素
      if (k == key)
          return e;
      // ThreadLocal为空,需要删除过期元素，同时进行rehash
      if (k == null)
          expungeStaleEntry(i);
      else
          i = nextIndex(i, len);
      e = tab[i];
  }
  return null;
}

线性探测法贯穿了get,set的所有流程，理解了原理在看代码就很简单了。

remove()方法

private void remove(ThreadLocal<?> key) {
   Entry[] tab = table;
   int len = tab.length;
   int i = key.threadLocalHashCode & (len-1);
   for (Entry e = tab[i];
        e != null;
        e = tab[i = nextIndex(i, len)]) {
       if (e.get() == key) {
           e.clear();
           expungeStaleEntry(i);
           return;
       }
   }
}

remove的时候回删除旧的entry,然后进行rehash.

ThreadLocal的使用

public class Counter {

  private static ThreadLocal<Integer> seqCount = new ThreadLocal<Integer>(){
    public Integer initialValue() {
        return 0;
    }
  };

  public int nextInt(){
    seqCount.set(seqCount.get() + 1);

    return seqCount.get();
  }
  public static void main(String[] args){
    Counter seqCount = new Counter();

    CountThread thread1 = new CountThread(seqCount);
    CountThread thread2 = new CountThread(seqCount);
    CountThread thread3 = new CountThread(seqCount);
    CountThread thread4 = new CountThread(seqCount);

    thread1.start();
    thread2.start();
    thread3.start();
    thread4.start();
  }

  private static class CountThread extends Thread{
    private Counter counter;

    CountThread(Counter counter){
        this.counter = counter;
    }

    @Override
    public void run() {
        for(int i = 0 ; i < 3 ; i++){
            System.out.println(Thread.currentThread().getName() + " seqCount :" + counter.nextInt());
        }
    }
  }
}

运行效果如下：

Thread-3 seqCount :1
Thread-0 seqCount :1
Thread-3 seqCount :2
Thread-0 seqCount :2
Thread-0 seqCount :3
Thread-2 seqCount :1
Thread-2 seqCount :2
Thread-1 seqCount :1
Thread-3 seqCount :3
Thread-1 seqCount :2
Thread-1 seqCount :3
Thread-2 seqCount :3

ThreadLocal 其实是为每个线程都提供一份变量的副本, 从而实现同时访问而不受影响。从这里也看出来了它和synchronized之间的应用场景不同, synchronized是为了让每个线程对变量的修改都对其他线程可见, 而 ThreadLocal 是为了线程对象的数据不受其他线程影响, 它最适合的场景应该是在同一线程的不同开发层次中共享数据。