优先级队列(PriorityQueue)源码解析

什么是堆

Java中的PriorityQueue采用的是堆这种数据结构来实现的,而存储堆采用的则是数组。

二叉树当中，叶子节点全部在最底层，除了叶子节点外,每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

如果叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树就叫作完全二叉树。

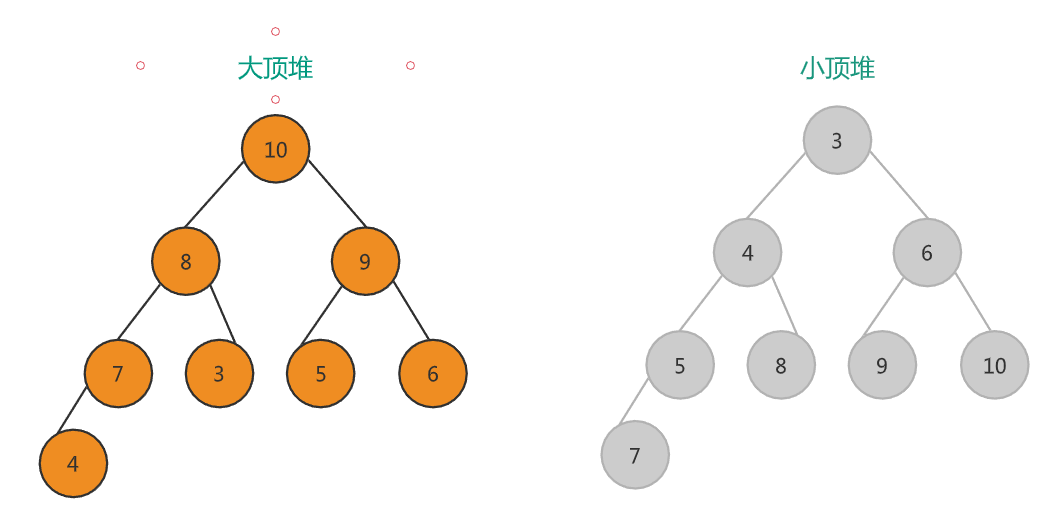
堆是一个完全二叉树,堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值,对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做大顶堆，对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做小顶堆。

如何实现一个堆

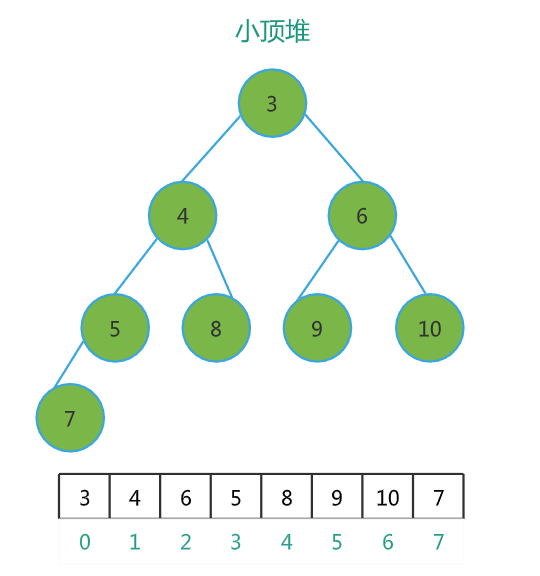
可以看出来，数组中下标为i的节点，其左子节点就是下标为 i*2+1 的节点,右子节点则是下标为 i*2+2 的节点。

PriorityQueue数据结构如下:

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {
  
  private static final int DEFAULT_INITIAL_CAPACITY = 11;

  // 数组
  transient Object[] queue;

  // 数组中元素个数
  private int size = 0;

}

建堆

我们一般对堆中数据的操作无非是新增元素和删除元素,当做这两个操作的时候,需要继续满足堆的两个特性，不可避免就需要重建堆,这个过程叫做堆化。

新增

新增的时候，我们将插入的数据暂时放置到数组中的最后一个位置，运气好的话,它就刚好满足堆特性，也不需要移动元素了。不好的话就需要移动元素位置了。

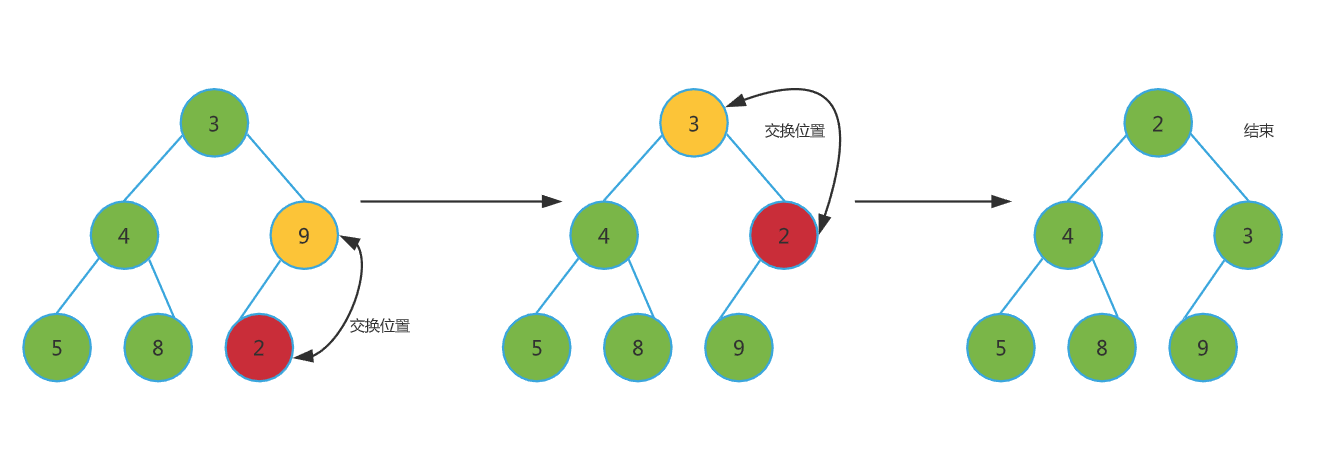
移动过程如下：新插入的节点与父节点比较大小，如果不满足子节点大于等于父节点的大小关系(小顶堆)，则互换两个节点，一直重复这个过程，直到父子节点满足刚才说的那种关系

 public boolean offer(E e) {
  if (e == null)
      throw new NullPointerException();
  modCount++;
  int i = size;
  if (i >= queue.length)
      grow(i + 1);
  size = i + 1;

  // 第一次插入放入数组的第一个位置(下标从0开始)
  if (i == 0)
      queue[0] = e;
  else
      siftUp(i, e);
  return true;
}

// 堆化过程
private void siftUpComparable(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>) x;
  while (k > 0) {
    
    // 1. 父节点位置 (k-1)/2,这里采用无符号右移(值为整数)
    int parent = (k - 1) >>> 1;
    Object e = queue[parent];
    // 2. 如果要插入的元素大于父节点元素的值，则结束堆化过程
    if (key.compareTo((E) e) >= 0)
        break;
    // 3. 交换元素位置
    queue[k] = e;
    k = parent;
  }
  queue[k] = key;
}

总结下插入元素时的主要过程

判断插入元素是否为空，为空则抛出NPE异常
在判断数组是否需要扩容,如果是则进行扩容
如果是第一次插入元素，则放入数组的第一个位置
如果不是则进行堆化过程
1. 找到父节点位置 : (k-1) >>> 1
2. 判断插入元素的值是否大于父节点(小顶堆)，如果是则结束堆化过程
3. 如果不是则交换元素位置
4. 持续上面的1,2,3步骤，直到插入的节点已经是堆顶结点(k==0)

删除

对于小顶堆而言,当删除堆顶元素之后，就需要把第二小的元素放到堆顶,那么第二小的元素就会出现在左右子节点中。当删除后，如果我们还是迭代的从左右子节点中选择最小元素放入堆顶，就会造成数组空洞，我用下面的图来演示这个问题。

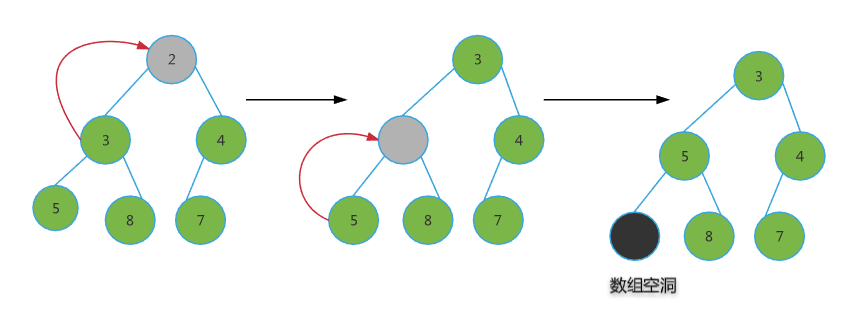
那怎么办？我们发现由于删除了一个元素,所以在移动的过程中会导致空洞，那么能不能找一个元素把这个洞填起来呢？当然莫问题啦。

我们可以在删除堆顶元素的时候，将最后一个元素拿来补位。由于在堆化的过程中，都是交换操作，就不会出现数组空洞了。

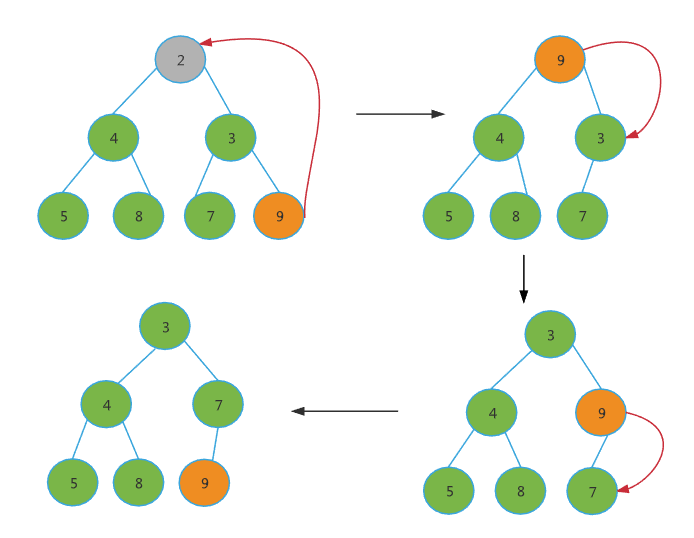
我们在来看看源码中是如何写的

// k=0, x=queue[size-1]
 private void siftDownComparable(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>)x;
  int half = size >>> 1;        // loop while a non-leaf
  while (k < half) {
      int child = (k << 1) + 1; // assume left child is least

      // 找到左右子节点中小的那个节点
      Object c = queue[child];
      int right = child + 1;
      if (right < size &&
          ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
          c = queue[child = right];
      // 如果比小的那个节点值还要小,则循环结束
      if (key.compareTo((E) c) <= 0)
          break;
      // 移动数据
      queue[k] = c;
      k = child;
  }
  queue[k] = key;
}

需要注意的是这里的结束条件是k < half,为什么呢？因为我们的堆化是从上到下，只会找一边(要么是左子树，要么是右子树)。

大顶堆如何实现

我们上面的例子中举例的是小顶堆，那么大顶堆PriorityQueue支持吗？当然支持，我们可以在构造函数中传入Comparator来指定。

  PriorityQueue<Integer> queue = new PriorityQueue<Integer>(new Comparator<Integer>() {
      public int compare(Integer o1, Integer o2) {
          return o2 - o1;
      }
  });

  queue.add(2);
  queue.add(4);
  queue.add(3);
  queue.add(5);

  while(queue.size() > 0) {
      System.out.println(queue.poll());
  }

// 5  4  3  2